Розкладання числа на прості множники має кілька корисних застосувань: Визначення взаємної простоти: - Якщо два числа розкладені на прості множники, то їх взаємна простота визначається на основі того, чи мають вони спільні прості множники. Знаходження найбільшого спільного дільника (НСД): - Якщо два числа розкладені на прості множники, то їх НСД можна знайти, вибираючи прості множники, які є спільними для обох чисел, і множачи їх разом. Знаходження найменшого спільного кратного (НСК): - Розкладання чисел на прості множники також допомагає знайти їх НСК, вибираючи всі прості множники з їх максимальними степенями. Визначення дільників числа: - Розкладання на прості множники може допомогти визначити всі можливі дільники числа, що, в свою чергу, корисно при розв'язанні завдань факторизації. Роз'яснення структури числа: - Розкладання на прості множники дозволяє зрозуміти структуру числа, його складові частини та можливі взаємодії з іншими числами. Ці застосування розкладання числа на прості множники допомагають в різних областях математики, включаючи теорію чисел, криптографію, комбінаторику та інші.
приклад
Розкладання
на множники
Вибір
приклади
теорія

рішення

таймер

пояснення

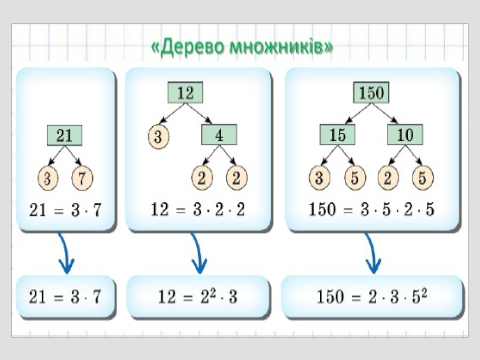
заставка
Кожне натуральне число, більше одиниці, має кілька дільників і може бути представлене у вигляді добутку його дільників.
Представлення числа у вигляді добутку натуральних чисел називають розкладанням на множники
Множники можуть бути простими або складеними числами
Представлення складеного числа у вигляді добутку, усі множники якого прості числа, називають розкладанням числа на прості множники.

Для розкладання числа на прості множники використовуючи наступні алгоритми.
Спосіб 1
Записуємо число у вигляді добутку двох довільних множників. Якщо один з множників — складене число, розкладуємо його знову на множники і т.д.
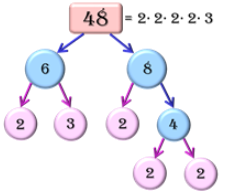
приклад 1
Спосіб 2
Проведемо вертикальну риску і записуємо зліва від неї ділене, а справа найменший простий дільник цього числа.
Частку записуємо зліва від риски під діленим. Кожний наступний дільник записуємо під попереднім в порядку зростання.
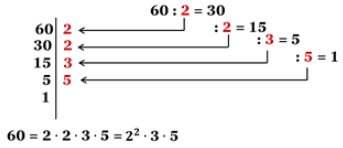
приклад 2

Складене число дорівнює добутку простих множників, на які це число розкладене.
Будь-яке складене число може бути розкладене на прості множники єдиним способом.
Наступний приклад
старт